list of all geometry formulas pdf

Geometry formulas, encompassing two and three-dimensional shapes, are essential for various calculations. A comprehensive geometry formulas PDF provides a readily available resource, including rectangle, circle, and cube formulas.
What is Geometry?
Geometry is a branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogs. It fundamentally deals with shape, size, relative position of figures, and the properties of space. Understanding geometry requires familiarity with formulas for calculating perimeter, area, volume, and other key characteristics of diverse shapes.
A geometry formulas PDF serves as a vital tool, consolidating these essential relationships. From basic two-dimensional forms like rectangles and circles to complex three-dimensional objects like spheres and cones, these formulas provide a systematic approach to problem-solving and spatial reasoning.
Importance of Geometry Formulas
Geometry formulas are crucial across numerous disciplines, extending beyond pure mathematics into fields like engineering, architecture, physics, and computer graphics. They enable precise calculations for construction, design, and analysis of spatial structures. A readily accessible geometry formulas PDF streamlines problem-solving, reducing errors and enhancing efficiency.
Mastering these formulas fosters critical thinking and analytical skills. Whether determining the area of a field, the volume of a container, or the dimensions of a building, these tools provide a foundational understanding of the world around us, making a comprehensive resource invaluable.
Where to Find a Comprehensive Geometry Formulas PDF
Numerous online resources offer comprehensive geometry formulas PDFs. Websites like mathportal.org and those listed within Chandler-Gilbert Community College’s Learning Center resources provide downloadable guides. Searching for “geometry formula sheet” or “geometry handbook” yields various options, including those from Mater Academy Charter Middle/High School.
Additionally, Earl Whitney’s resources (copyright 2010-2023) and mathworld.wolfram.com are excellent sources. Always verify the accuracy and completeness of any downloaded PDF, ensuring it covers the necessary shapes and concepts for your specific needs.

Two-Dimensional Shapes ⏤ Formulas
Two-dimensional shapes, like rectangles, squares, triangles, and circles, have specific formulas for perimeter and area, readily available in geometry formula PDFs.
Rectangle Formulas
Rectangle formulas are fundamental in geometry, easily accessible within a geometry formulas PDF. The perimeter, representing the total distance around the rectangle, is calculated as P = 2ℓ + 2w, where ℓ is the length and w is the width.
Conversely, the area, defining the space enclosed within the rectangle, is determined by A = ℓw. These simple yet powerful formulas are crucial for solving various problems involving rectangular shapes. Understanding these concepts, often found in readily available resources, is key to mastering basic geometric principles.
Perimeter of a Rectangle
The perimeter of a rectangle, a key formula found in any comprehensive geometry formulas PDF, represents the total distance around its four sides. It’s calculated by summing the lengths of all sides. Since a rectangle has two lengths (ℓ) and two widths (w), the formula is expressed as P = 2ℓ + 2w.
This straightforward calculation is essential for applications like fencing, framing, or determining the amount of material needed to enclose a rectangular area. Mastering this formula, readily available in reference materials, is a foundational step in geometric understanding.
Area of a Rectangle
The area of a rectangle, a fundamental concept detailed in any useful geometry formulas PDF, defines the space enclosed within its boundaries. It’s determined by multiplying the rectangle’s length (ℓ) by its width (w). Therefore, the formula is simply A = ℓw.
Understanding this calculation is crucial for tasks like flooring, tiling, or calculating the size of a rectangular garden. A clear grasp of this formula, easily accessible in reference guides, forms a cornerstone of geometric problem-solving and practical applications.
Square Formulas
A square, a special case of a rectangle, possesses unique formulas readily found within a comprehensive geometry formulas PDF. Because all sides are equal (denoted as ‘S’), calculations are simplified. Understanding these formulas is vital for various applications, from construction to design.
These formulas allow for efficient calculation of a square’s dimensions. A reliable geometry formulas PDF will clearly outline both perimeter and area, providing a quick reference for students and professionals alike. Mastering these concepts builds a strong foundation in geometric principles.
Perimeter of a Square
The perimeter of a square, representing the total distance around its four equal sides, is a fundamental calculation detailed in any good geometry formulas PDF. Since all sides are equal, denoted as ‘S’, the formula simplifies to P = 4S. This straightforward equation allows for quick determination of the square’s perimeter.
A readily accessible geometry formulas PDF will showcase this formula prominently. Understanding this concept is crucial for applications like fencing, framing, or any scenario requiring measurement of a square’s boundary. Accurate perimeter calculation ensures precise material estimation and project execution.
Area of a Square
Determining the area of a square, the space enclosed within its boundaries, is a core concept found within any comprehensive geometry formulas PDF. The formula, A = S², elegantly expresses this calculation, where ‘S’ represents the length of one side. Squaring the side length provides the area in square units.
A well-organized geometry formulas PDF will clearly display this formula for easy reference. This calculation is vital in fields like construction, landscaping, and design, where quantifying surface area is essential. Accurate area determination ensures efficient resource allocation and precise project planning.
Triangle Formulas
Triangle formulas are fundamental components of any complete geometry formulas PDF. These formulas enable the calculation of a triangle’s perimeter and area, crucial for diverse applications. The perimeter, P = a + b + c, simply sums the lengths of all three sides (a, b, and c).
Calculating the area, A = 1/2bh, requires knowing the base (b) and corresponding height (h). A comprehensive geometry formulas PDF will present these clearly. Understanding these formulas is essential for fields like engineering, architecture, and surveying, where triangular shapes frequently appear.
Perimeter of a Triangle
The perimeter of a triangle, a key element within any useful geometry formulas PDF, represents the total distance around its exterior. It’s calculated by simply adding the lengths of all three sides together. If the sides are denoted as ‘a’, ‘b’, and ‘c’, the formula is expressed as P = a + b + c.
This straightforward calculation is foundational for various geometric problems. A well-organized geometry formulas PDF will clearly display this formula alongside diagrams for easy comprehension. Mastering this concept is crucial for understanding more complex shapes and their properties.
Area of a Triangle (Base and Height)
Determining the area of a triangle, a staple in any comprehensive geometry formulas PDF, requires knowing its base and height. The formula is A = 1/2 * b * h, where ‘b’ represents the base length and ‘h’ signifies the perpendicular height. This formula efficiently calculates the space enclosed within the triangle’s boundaries.
A quality geometry formulas PDF will visually illustrate this concept, aiding understanding. Understanding this calculation is fundamental for solving problems involving land surveying, construction, and various mathematical applications. Accurate application of this formula is essential for precise results.
Circle Formulas
A complete geometry formulas PDF must include essential circle calculations. The circumference, representing the distance around the circle, is calculated using C = 2πr, where ‘r’ denotes the radius. The area, defining the space enclosed within the circle, is determined by A = πr2. These formulas are foundational for understanding circular shapes.
These formulas, readily available in any good geometry formulas PDF, are crucial in fields like engineering and architecture. Mastering these calculations allows for accurate determination of circular dimensions and areas, vital for practical applications and problem-solving.
Circumference of a Circle
As detailed in a comprehensive geometry formulas PDF, the circumference of a circle—the distance around it—is calculated using the formula C = 2πr. Here, ‘π’ (pi) is a mathematical constant approximately equal to 3.14159, and ‘r’ represents the circle’s radius. Alternatively, knowing the diameter (d), the circumference can be found using C = πd.
This formula, consistently found within any reliable geometry formulas PDF, is fundamental for various applications, from calculating the length of fencing around a circular garden to determining the distance a wheel travels in one rotation. Accurate circumference calculation is essential in numerous fields.
Area of a Circle
A readily available geometry formulas PDF will clearly state that the area of a circle—the space enclosed within its boundary—is determined by the formula A = πr². Here, ‘π’ (pi) remains the constant approximately equal to 3.14159, and ‘r’ signifies the radius of the circle. Squaring the radius and multiplying by pi yields the area.
This crucial formula, consistently included in any complete geometry formulas PDF, is vital for calculations involving circular regions, such as determining the amount of material needed to cover a circular surface or calculating the capacity of a circular pool.
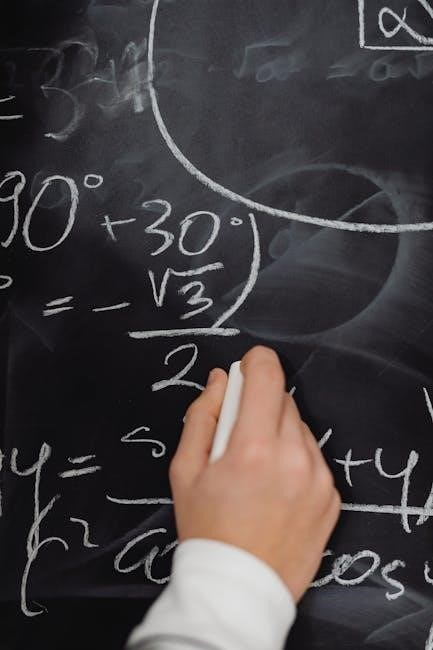
Parallelogram Formulas
A comprehensive geometry formulas PDF details that parallelograms, possessing opposite sides parallel, have specific formulas for perimeter and area. The perimeter, representing the total length of all sides, is calculated as P = 2a + 2b, where ‘a’ and ‘b’ denote the lengths of adjacent sides.
Crucially, the area of a parallelogram—the space it encloses—is determined by A = bh, where ‘b’ represents the base length and ‘h’ signifies the perpendicular height. Any reliable geometry formulas PDF will consistently present these formulas for quick reference and accurate calculations.
Perimeter of a Parallelogram
As detailed in a standard geometry formulas PDF, the perimeter of a parallelogram is found by summing the lengths of all its sides. Because opposite sides of a parallelogram are equal in length, the formula simplifies to P = 2a + 2b. Here, ‘a’ and ‘b’ represent the lengths of the adjacent sides.
Essentially, you add the length of one pair of parallel sides to the length of the other pair. A well-organized geometry formulas PDF will clearly illustrate this, providing a quick and easy reference for students and professionals alike when calculating the perimeter.
Area of a Parallelogram
According to most geometry formulas PDF resources, the area of a parallelogram is determined by multiplying the base length by the height. The formula is expressed as A = b * h, where ‘b’ represents the base and ‘h’ signifies the perpendicular height.
It’s crucial to remember that the height isn’t the length of the slanted side; it’s the perpendicular distance between the base and its opposite side. A comprehensive geometry formulas PDF will often include a diagram to visually demonstrate this concept, aiding in accurate calculations and understanding.
Trapezoid Formulas
A geometry formulas PDF will detail that a trapezoid’s perimeter is found by summing all four sides: P = a + b + c + d, where a, b, c, and d are the lengths of each side. However, calculating the area requires a different approach.
The area of a trapezoid, as outlined in most geometry formulas PDF guides, is calculated using the formula A = ½ * (b₁ + b₂) * h, where b₁ and b₂ represent the lengths of the two parallel sides (bases), and ‘h’ is the perpendicular height between them. Understanding this distinction is key.
Perimeter of a Trapezoid
As detailed in a standard geometry formulas PDF, the perimeter of a trapezoid is simply the sum of the lengths of all its sides. This means adding together the lengths of the two parallel sides (often labeled ‘a’ and ‘b’) and the lengths of the two non-parallel sides (labeled ‘c’ and ‘d’).
Therefore, the formula for the perimeter (P) is expressed as: P = a + b + c + d. A helpful geometry formulas PDF will visually represent this, making it easier to understand. This straightforward calculation is a fundamental concept in two-dimensional geometry;
Area of a Trapezoid
According to most geometry formulas PDF resources, calculating the area of a trapezoid requires knowing the lengths of its parallel sides (a and b) and its height (h) – the perpendicular distance between those sides. The formula isn’t simply an addition, but involves multiplication and division.
The area (A) is calculated as: A = 1/2 * (a + b) * h. A comprehensive geometry formulas PDF will illustrate this with a diagram. Essentially, you average the lengths of the parallel sides and then multiply by the height. This formula is crucial for solving various geometric problems.

Three-Dimensional Shapes ⏤ Formulas
Geometry formulas PDF resources detail shapes like cubes, spheres, cylinders, and cones. These formulas calculate surface area and volume, vital for spatial understanding.
Cube Formulas
A cube, a fundamental three-dimensional shape, possesses six equal square faces. A geometry formulas PDF will clearly outline its properties. Calculating its surface area requires understanding all six faces; the formula is 6s², where ‘s’ represents the side length. Determining the cube’s volume is equally straightforward, utilizing the formula s³.
These formulas are crucial in various applications, from calculating the capacity of containers to determining material requirements in construction. Accessing a reliable geometry formulas PDF ensures accurate calculations for both surface area and volume, simplifying complex spatial problems. Mastering these formulas unlocks a deeper understanding of three-dimensional geometry.
Surface Area of a Cube
The surface area of a cube, readily available in any comprehensive geometry formulas PDF, represents the total area of all its six identical square faces. Calculating this involves determining the area of a single face (side * side, or s²) and then multiplying by six. Therefore, the formula is 6s², where ‘s’ denotes the length of one side of the cube.
Understanding this formula is vital for applications like calculating the amount of material needed to construct a cube-shaped object or determining the surface available for painting. A well-organized geometry formulas PDF will present this clearly, aiding in quick and accurate calculations.

Volume of a Cube
Determining the volume of a cube, a fundamental concept detailed in any complete geometry formulas PDF, signifies the amount of space it occupies. This is calculated by cubing the length of one of its sides. The formula, succinctly expressed as s³, where ‘s’ represents the side length, provides a straightforward method for volume calculation.
This formula finds practical application in scenarios like determining the capacity of a cube-shaped container or calculating the amount of material required to fill it. A readily accessible geometry formulas PDF ensures quick reference and accurate results for these types of problems.
Sphere Formulas
A geometry formulas PDF will invariably include formulas for spheres, perfectly symmetrical three-dimensional objects. Calculating a sphere’s surface area requires the formula 4πr², where ‘r’ denotes the radius. Determining its volume utilizes the formula (4/3)πr³, again dependent on the radius.
These formulas are crucial in fields like physics and engineering, for instance, calculating the volume of a spherical tank or the surface area exposed to fluid flow. A comprehensive geometry formulas PDF provides these essential tools, ensuring accurate calculations and efficient problem-solving in diverse applications;
Surface Area of a Sphere
A readily available geometry formulas PDF will clearly state the surface area of a sphere is calculated using the formula 4πr², where ‘r’ represents the sphere’s radius. This formula determines the total area covering the sphere’s outer surface.
Understanding this formula is vital in various applications, from calculating material requirements for spherical objects to determining heat transfer rates. A good geometry formulas PDF will not only present the formula but may also include illustrative examples, aiding comprehension and practical application. Accurate calculation relies on correctly identifying and applying this fundamental formula.
Volume of a Sphere
A comprehensive geometry formulas PDF will detail the volume of a sphere as (4/3)πr³, where ‘r’ signifies the sphere’s radius. This formula calculates the amount of three-dimensional space enclosed within the sphere’s surface. It’s a crucial calculation in physics and engineering.
Access to a reliable geometry formulas PDF ensures accurate volume determination for spherical objects. Understanding the formula’s components – the constant 4/3, pi (π), and the radius cubed – is essential. Practical applications range from calculating the capacity of spherical tanks to determining the mass of celestial bodies.
Cylinder Formulas
A detailed geometry formulas PDF outlines cylinder calculations. The surface area is 2πrh + 2πr², where ‘r’ is the radius and ‘h’ the height. This accounts for the curved surface and two circular bases. The volume, crucial for capacity calculations, is given by πr²h.

Consulting a geometry formulas PDF ensures accurate results when working with cylindrical shapes. These formulas are fundamental in engineering, architecture, and everyday applications like determining the volume of containers. Mastering these calculations simplifies complex spatial problems, providing a solid foundation for further mathematical exploration.
Surface Area of a Cylinder
A geometry formulas PDF clearly states the surface area of a cylinder as 2πrh + 2πr²; This formula, essential for calculating the total area covering the cylinder, comprises the lateral surface area (2πrh) and the areas of the two circular bases (2πr²).
Referencing a reliable geometry formulas PDF ensures correct application. Understanding this formula is vital in fields like manufacturing and packaging, where material requirements are critical. Accurate surface area calculations minimize waste and optimize resource allocation, demonstrating the practical value of these geometric principles.
Volume of a Cylinder
A comprehensive geometry formulas PDF defines the volume of a cylinder as πr²h. This crucial formula calculates the capacity of the cylinder, representing the space it encloses. The formula multiplies the area of the circular base (πr²) by the height (h) to determine the total volume.
Consulting a reliable geometry formulas PDF guarantees accurate calculations. This is particularly important in engineering and physics, where precise volume measurements are frequently required. Understanding this formula aids in determining liquid capacity, material usage, and overall design considerations, showcasing its practical significance.
Cone Formulas
A detailed geometry formulas PDF outlines the calculations for cones, encompassing both surface area and volume. The volume of a cone is determined by the formula (1/3)πr²h, where ‘r’ represents the radius of the base and ‘h’ signifies the height. This formula, readily available in any comprehensive geometry formulas PDF, is fundamental for various applications.
Accessing a reliable geometry formulas PDF ensures accurate calculations for conical structures. These calculations are vital in fields like architecture and engineering. Understanding the cone’s volume allows for precise material estimation and structural analysis, demonstrating its practical importance in real-world scenarios.
Surface Area of a Cone
A comprehensive geometry formulas PDF details the calculation of a cone’s surface area, which comprises the base area and the lateral surface area. The formula is πr(r + l), where ‘r’ is the radius and ‘l’ represents the slant height. Finding this information within a geometry formulas PDF is crucial for accurate calculations.
Understanding this formula, readily available in any good geometry formulas PDF, is essential for determining the material needed to cover the cone’s exterior. This is particularly important in manufacturing and design. Accurate surface area calculations ensure efficient resource allocation and minimize waste, showcasing its practical value.
Volume of a Cone
A detailed geometry formulas PDF provides the formula for calculating a cone’s volume: (1/3)πr²h, where ‘r’ denotes the radius of the circular base and ‘h’ represents the cone’s perpendicular height. Accessing this formula within a geometry formulas PDF simplifies complex spatial calculations.
This formula, consistently found in any reliable geometry formulas PDF, is vital in various applications, including engineering and architecture. Determining the volume accurately is crucial for tasks like calculating capacity or material requirements. A readily available geometry formulas PDF ensures quick and precise results, enhancing efficiency and accuracy.

Analytic Geometry Formulas
Analytic geometry formulas, often found in a geometry formulas PDF, define lines and circles using coordinate systems, including slope-intercept and two-point forms.
Lines in Two Dimensions
Understanding lines within a two-dimensional plane is fundamental in analytic geometry, and readily available within a comprehensive geometry formulas PDF. Key formulas define these lines based on known points and characteristics; The slope-intercept form (y = mx + b) expresses a line’s equation using its slope (m) and y-intercept (b). Alternatively, the two-point form calculates the line’s equation given two points on the line, utilizing their coordinates.
Furthermore, the point-slope form defines a line using a point and its slope. These formulas are crucial for determining line equations, calculating distances, and analyzing geometric relationships, all conveniently summarized in a dedicated resource.
Slope-Intercept Form
The slope-intercept form, a cornerstone of analytic geometry detailed in any good geometry formulas PDF, elegantly represents a linear equation as y = mx + b. Here, ‘m’ signifies the line’s slope – its steepness and direction – while ‘b’ represents the y-intercept, the point where the line crosses the y-axis.
This form simplifies determining a line’s characteristics and plotting it on a coordinate plane. Knowing the slope and y-intercept allows for quick and accurate graphical representation. It’s a fundamental tool for solving linear equations and understanding relationships between variables, often found within comprehensive formula collections.
Two-Point Form
The two-point form, crucial for defining a line when two points are known, is detailed within any complete geometry formulas PDF. This form is expressed as (y ― y1) = [(y2 ⏤ y1) / (x2 ― x1)] * (x ⏤ x1). It calculates the slope using the coordinates of the two given points (x1, y1) and (x2, y2).
This formula is particularly useful when the slope isn’t immediately apparent. It allows for direct calculation of the line’s equation, facilitating problem-solving in coordinate geometry. Mastering this form is essential for a thorough understanding of linear relationships, as presented in comprehensive geometry resources.
Circles ⏤ Properties and Formulas
A comprehensive geometry formulas PDF details essential circle properties. Key theorems include the Tangent-Chord Theorem (angle formed by tangent and chord equals inscribed angle) and the Tangent-Secant Theorem (external segment squared equals whole secant times external segment). These properties are vital for solving complex geometric problems.
Formulas cover circumference (C = 2πr) and area (A = πr2). Understanding these relationships, alongside theorems concerning tangents and chords, provides a strong foundation in circle geometry. These concepts are frequently tested and are crucial for success in mathematical applications.
Tangent-Chord Theorem
A detailed geometry formulas PDF will illustrate the Tangent-Chord Theorem. This theorem states that the angle formed by a tangent and a chord at the point of tangency is equal to the inscribed angle subtended by the same chord. This relationship, often denoted as x n, is fundamental in circle geometry.
Understanding this theorem allows for the calculation of unknown angles and lengths within a circle. It’s frequently used in conjunction with other circle theorems to solve complex problems. Visual aids within the PDF will demonstrate the theorem’s application with labeled diagrams, clarifying its practical use.
Tangent-Secant Theorem
A comprehensive geometry formulas PDF details the Tangent-Secant Theorem, a crucial concept in circle geometry. This theorem establishes a relationship between a tangent segment and a secant segment drawn to a circle from an external point. Specifically, the square of the length of the tangent segment (a2) equals the product of the external secant segment and the entire secant segment (b(b+c)).
This theorem, often represented as a2 = b(b+c), is vital for solving problems involving lengths of tangent and secant segments. Diagrams within the PDF will visually demonstrate this relationship, aiding in comprehension and application.